공부해서 남주자

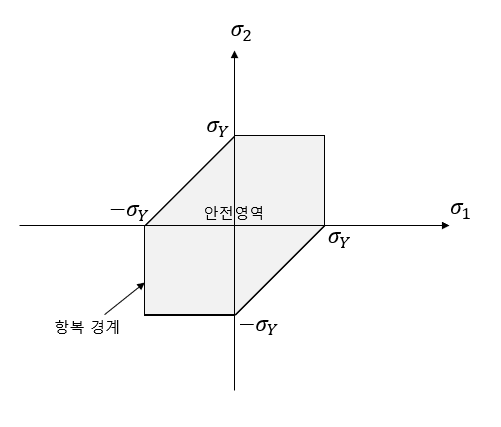
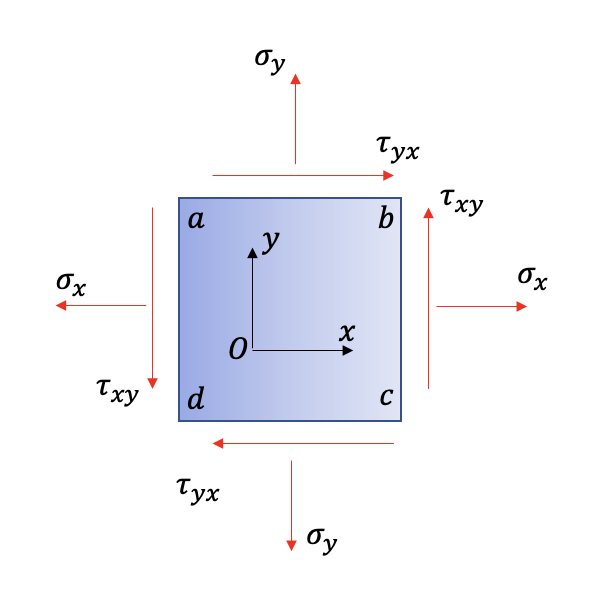
이번 포스팅에서는 파손 이론에 대한 내용 중 정적파손에 대해 먼저 알아보도록 하겠습니다. 파손(failure) 이론이란? 파손은 부품이 두개 혹은 그 이상으로 분리되거나 모양이 바뀌어 부품의 원래 기능을 제대로 할 수 없게 된 상태를 말합니다. 파손은 정하중 상태에서 발생하는 정적파손과 동하중 상태에서 발생하는 피로파손으로 나뉩니다. 그리고 파손 이론은 이러한 파손현상을 복잡한 형상의 부품으로 실험하지 않고 단축인장실험 데이터로 어떻게 입체에 써먹을까 하는 것을 말합니다. 정적 파손(static failure) 정적 파손에 대하여 일반적으로 잘 쓰이는 세가지 이론에 대해 알아보겠습니다. (1) 최대 전단응력 이론(maximum shear stress theory) 최대 전단응력 이론은 기계부품의 최대 전..

이번 포스팅에서는 재료의 파손을 설명하기 위한 이론 중 하나인 전단변형에너지 이론에 쓰이는 전단변형에너지 공식을 유도해보겠습니다. 전단변형에너지 이론? 전단변형에너지 이론은 von mises 이론이라고도 불리며, 재료의 파손을 설명하기 위해 제안된 이론 중 하나입니다. 재료의 파손에 대한 내용은 추후 포스팅에서 설명드리도록 하겠으며, 본 포스팅에서는 해당 이론에 쓰이는 전단변형에너지 공식을 유도해보겠습니다! 전단변형에너지 공식 유도 전단변형에너지를 알기 위해서는 총 변형에너지와 체적변형에너지를 알아야 합니다. 전단변형에너지는 총 변형에너지에서 체적변형에너지를 뺀 값이기 때문이죠! $$ 전단변형에너지 = 총 변형에너지 - 체적변형에너지$$ 총 변형에너지 3차원 응력 상태에서 총 변형에너지는 아래와 같습니다..

이번 포스팅에서는 본 미세스 응력에 대하여 알아봅시다. 본 미세스 응력(von mises stress)이란? 부르기에 따라 본 미세스 응력, 폰 미세스 응력이라고 부르기도 하는 이 응력은 흔히 등가응력(equivalent stress)으로 불리는 특수한 목적을 가진 응력입니다. 물체가 하중을 받게 되면 더 이상 외력을 견디지 못하고 파괴되는 시점이 오는데, 이러한 파괴를 예측하는 기준이 되는 응력을 항복응력(Yield stress)이라고 하며, 이 항복응력의 대표적인 기준으로써 본 미세스 응력이 쓰입니다. 예를 들어 특정 지점에서 각 3개의 normal stress, shear stress가 발생할 때 각 응력 성분들만으로는 물체가 외부하중에 의해 안전할지, 파괴될지를 판단할 수 없습니다. 이 때 각 응..

이번 포스팅에서는 원통형 압력용기에서의 응력에 대해 알아보겠습니다. 원통형 압력용기에서의 응력 아래의 그림을 바탕으로 원주 방향과 길이 방향의 응력을 각각 구해봅시다. 원주 방향 응력 우선 용기의 벽에 작용하는 원주응력 $\sigma _{1}$과 내부 압력에 의한 합성력 $P_{1}$에 대해 평형방정식을 세워볼 수 있습니다. $$\sigma _{1}(2bt)-2pbr=0$$ 이 식으로부터 원통형 압력용기에서의 원주방향 응력을 구할 수 있습니다. $$\sigma _{1} = \frac{pr}{t}$$ 길이 방향 응력 길이 방향 응력 $\sigma _{2}$의 합력은 $\sigma _{2}(2\pi rt)$와 같고 내압에 의한 합력 $P_{2}=p\pi r^{2}$와 평형을 이루어야 합니다. 즉, $$ \s..

이번 포스팅에서는 압력용기에서의 응력에 대해 알아봅시다. 구형 압력용기에서의 응력 구형 용기 내의 응력을 결정하기 위해 구를 수직 지름 평면으로 자르고, 용기의 절반과 내용물에 의한 압력을 자유물체도로 그리면 아래 그림과 같습니다. 압력은 균일하게 작용하므로 반구 내에 남아있는 유체의 평면 원형 면적에 작용하는 힘 $P$는 아래와 같습니다. $$P = p(\pi r^{2})$$ 그리고 용기와 하중의 대칭성으로 인해 인장응력 $\sigma$는 원주방향으로 균일합니다. 그렇기 때문에 이를 이용하여 벽 내부에 작용하는 인장응력의 합력은 응력과 이 응력이 작용하는 면적을 곱한 것과 같습니다. 즉, $$\sigma (2\pi r_{m}t)$$ 여기서 $t$는 벽의 두께이고, $r_{m}$은 $r+\frac{t}{..

이번 포스팅에서는 모어 원(Mohr's circle)에 대해 알아봅시다. 모어 원(Mohr's circle) 평면응력에서의 변환 공식은 모어원으로 쉽게 나타낼 수 있습니다. 모어 원은 응력을 받는 점에서 여러 경사면에 작용하는 수직 및 전단응력의 관계를 그림으로 보여주기 때문에 이해하는데에 매우 쉽습니다. 모어 원의 방정식 모어 원의 방정식은 평면응력을 다뤘던 공식을 변형하여 구할 수 있습니다. [재료역학] 평면응력(plane stress) 및 경사면에서의 응력 이번 포스팅에서는 평면응력이 무엇인지, 그리고 경사면에서의 응력은 어떻게 구하는지에 대해 알아보겠습니다. 평면응력(plane stress) 재료의 $x, y$면에만 응력이 작용하고 모든 응력은 $x$축 및 study2give.tistory.com..

이번 포스팅에서는 평면응력이 무엇인지, 그리고 경사면에서의 응력은 어떻게 구하는지에 대해 알아보겠습니다. 평면응력(plane stress) 재료의 $x, y$면에만 응력이 작용하고 모든 응력은 $x$축 및 $y$축에 평행하고 작용한다고 했을 때, 이러한 응력의 상태를 평면응력상태라고 합니다. 평면응력은 인장과 압축을 받는 봉, 비틀림을 받는 축 등을 해석할 때 유용합니다. 경사면에서의 응력 경사면에서의 응력을 설명하기 위해서는 아래와 같은 사각형 요소를 고려해야 합니다. 위 그림에서 요소가 $\theta$만큼 기울었을 때 경사단면에 작용하는 응력을 구해봅시다. $\theta$만큼 기울어진 상태의 응력은 이미 알고있는 $\sigma _{x}, \sigma _{y}, \tau _{xy}$를 이용해 구할 수 ..

이번 포스팅에서는 동력을 계산하는 방법을 알아봅시다. 일(work)과 동력(power) 일반적으로 일정 토크에 의해 한 일(work)는 아래와 같이 계산할 수 있습니다. $$W=T\psi$$ 여기서 $\psi$는 회전각(rad)을 나타냅니다. 그럼 동력(power)는 일의 시간에 대한 변화율로 계산할 수 있으므로, $$P=\frac{dW}{dt} = T\frac{d\psi}{dt}$$ 로 나타낼 수 있습니다. 여기서 회전각의 변화율 $\frac{d\psi}{dt}$은 각 속도$\omega$를 나타내므로 정리하여 나타내면 동력은 아래와 같습니다. $$P=T\omega$$ 위 식을 이용해 일정한 토크 $T$를 전달하는 회전축에 의해 전달된 동력을 계산할 수 있습니다. 다양한 표현법(각속도 표현방법, 단위 등..

이번 포스팅에서는 순수전단(pure shear) 상태에 대해 알아보겠습니다. 순수전단(Pure shear) 우리는 비틀림을 받는 봉의 두 단면 사이를 잘라낸 응력요소를 고려하기 위해 순수전단(pure shear) 상태에 있는 구조물을 고려할 필요가 있습니다. 순수전단 상태에 있는 요소에 작용하는 유일한 응력은 아래 그림과 같이 네개 측면 위의 전단응력 $\tau$입니다. 여기서는 수직응력은 인장일 때 양(+), 전단응력은 수직면에 재료를 반시계방향으로 회젼시키려고 하는 힘을 양(+)으로 정의하겠습니다. 경사면에서의 응력 순수전단 상태에서는 응력 요소의 앞면과 뒷면에는 아무런 응력도 작용하지 않습니다. 따라서 모든 응력을 나타내면 아래그림과 같습니다. 경사면에서의 응력을 알고 싶을 때, 우리는 위 삼각형 ..

이번 포스팅에서는 비틀림(Torsion)에 대하여 알아보겠습니다. 비틀림(Torsion) 비틀림이란 봉의 길이방향 축에 대해 회전을 일으키려하는 모멘트에 의해 가해지는 현상을 말합니다. 만약 재료가 선형 탄성이면, 전단에 대한 훅의 법칙을 사용하여 비틀림 현상을 표현할 수 있습니다. 선형 탄성(linear elastic) 봉의 비틀림(torsion) 위에서 언급한대로, 만약 재료가 선형 탄성이면 전단에 대한 훅의 법칙을 사용할 수 있습니다. $$\tau = G\gamma$$ 여기서 $G$는 전단탄성계수이고 $\gamma$는 전단변형률입니다. 전단변형률을 좀 더 풀어서 식을 쓰면 아래와 같습니다. $$\tau _{max} = Gr\theta$$ $$\tau = G\rho\theta = \frac{\rho}..