공부해서 남주자

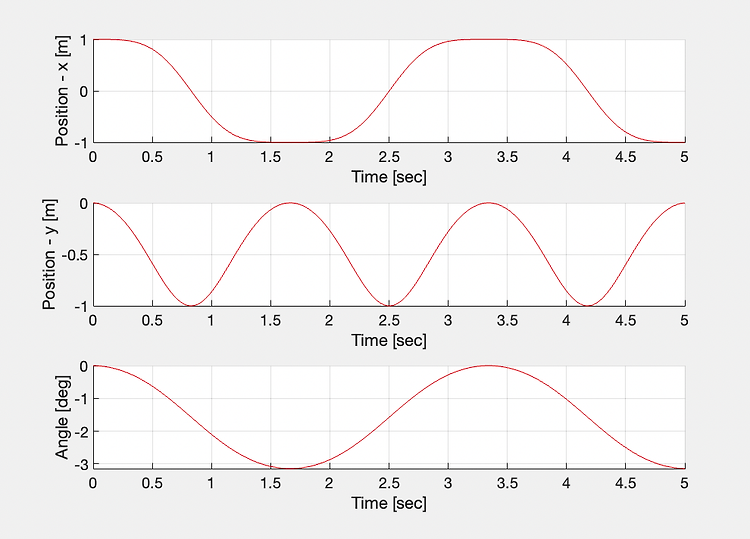
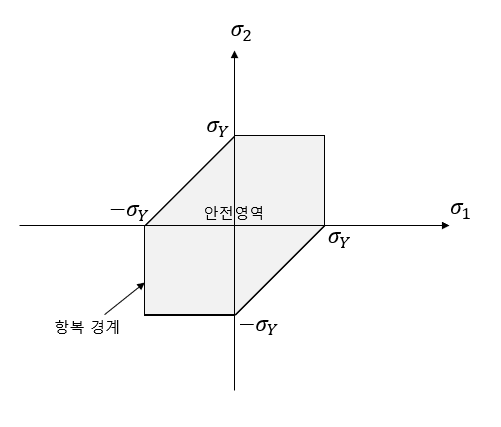
이번 포스팅에서는 오일러 각(Euler Angle)을 Python으로 구현해보겠습니다.  오일러 각(Euler Angle) 기본기본적인 내용은 아래 글에서 다룬 바 있습니다. 2020.11.19 - [공학/동역학] - [동역학] 오일러 각(Euler angle) [동역학] 오일러 각(Euler angle)이번 포스팅에서는 오일러 각에 대해 알아보도록 합시다. 오일러 각(Euler angle) 오일러 각은 흔히 오일러 앵글이라고들 많이 부르는데, 3차원 공간에서 강체가 놓인 자세를 표현하기 위해 나타내study2give.tistory.com 다시 한번 간단하게 설명하자면, 3차원 공간에서 강체가 놓인 자세를 표현하기 위해 나타내는 3개의 각도를 말하며, 3차원 공간에서는 각 축방향으로 회전하는 순서에 따라..

이번 포스팅에서는 Resampling의 개념과 예시에 대해 알아보겠습니다.  Resampling이란?Resampling은 원본 dataset의 sample을 다시 생성하는 것을 말하며, 주로 시계열 데이터에서 시간 간격을 재조정하기 위해 사용됩니다.   Resampling의 유형Resampling은 크게 두가지로 나눌 수 있는데요. 1. DownSampling   데이터의 빈도를 낮추는 방법을 말합니다.   예를 들어 초단위 데이터를 분단위로 변환한다거나,   0.01초 간격의 데이터를 0.1초 간격으로 변환하는 등의 방법이 있습니다. 2. UpSampling   이름에서 알 수 있듯이 위 방법과는 반대로 데이터의 빈도를 높이는 방법입니다.  위 두 방법에 대해 예시로 알아보겠습니다.   DownSamp..

이번 포스팅에서는 평면에서의 운동방정식에 대하여 알아보고, 구속이 포함된 운동방정식을 이용하여 단진자 운동 해석을 해보겠습니다. 자코비안 행렬(jacobian matrix) 앞선 포스팅에서 우리는 기구의 구속식에 대해 알아보았습니다. 구속식은 기본적으로 body의 좌표로 이루어져있기 때문에, 초기값이 주어지면 해당 구속식을 풀어 기구의 상태를 확정할 수 있습니다. 운동방정식을 구성하기 위해서는 이 구속식을 미분하여 속도, 가속도를 구할 필요가 있는데요. 이 때 구속식을 각 좌표로 편미분하여 변화량을 구한 행렬을 자코비안 행렬(jacobian matrix)이라 합니다. 구속식이 존재하는 기구의 운동방정식을 구성하기 위해서는 이 자코비안 행렬이 필수적입니다. 예를 들어 Revolute joint의 자코비안을..

이번 포스팅에서는 평면에서의 기구학에 대해 다뤄보겠습니다. 본문의 내용은 참고문헌의 내용을 참고한 것임을 밝힙니다. 참고문헌: Computer-aided analysis of mechanical systems, Parviz E. Nikravesh 평면 기구학(Planar kinematics) 평면에 임의의 body $i$가 존재한다면, 해당 body의 운동을 기술하기 위해서는 3개의 좌표가 필요합니다. $x_i, y_i, \phi_i$가 그것입니다. $x_i, y_i$는 평면 상의 위치를 나타내고, $\phi_i$는 얼마나 기울어져 있는지에 대한 자세를 나타냅니다. 위 그림에서 벡터 $r_i^P$는 아래와 같이 나타낼 수 있습니다. $$r_i^P = r_i+A_i s\prime_i^P \tag{1}$$ ..

이번 포스팅에서는 이전 포스팅에서 못다한 이야기를 해보겠습니다. 이전 포스팅을 확인하시려면 아래를 눌러주세요. [동역학] 오일러 파라미터(Euler parameters) - (1) 이번 포스팅에서는 오일러 파라미터에 대해 알아보겠습니다. (참고문헌: Computer-aided analysis of mechanical systems, Parviz E. Nikravesh) 오일러 파라미터(Euler parameters)란? 3차원 공간에서 구속되지.. study2give.tistory.com 오일러 파라미터를 활용하여 좌표변환행렬 구하기 이전 포스팅에서 아래와 같은 결과를 도출했었습니다. $$\overrightarrow{p}^T\overrightarrow{p}-1=0$$ 이 때, $\overrightarro..

이번 포스팅에서는 오일러 파라미터에 대해 알아보겠습니다. (참고문헌: Computer-aided analysis of mechanical systems, Parviz E. Nikravesh) 오일러 파라미터(Euler parameters)란? 3차원 공간에서 구속되지 않은 물체(unconstrained body)는 병진 3개 + 회전 3개, 총 6개의 좌표로 그 상태를 정의할 수 있습니다. 그리고 그 6개의 좌표는 global(x-y-z) 좌표계와 body-fixed($\xi-\eta-\zeta$) 좌표계의 관계로 정의할 수 있습니다. 이 때, 물체 위에 존재하는 모든 점은 body-fixed 좌표계에 놓여있기 때문에 global 좌표계를 기준으로도 정의할 수 있는데요. 이 관계를 설명하기 위한 수단이 ..

이번 포스팅에서는 기구학적 구속에 대해 알아보겠습니다. 기구학적 구속(kinematic constraint)과 구속식(constraint equation) 기구학적 구속이란 어떤 기구의 운동을 규정된 경계에 제한하거나 한정된 상태로 정의하는 것을 말하며, 이를 흔히 조인트(joint)라 부릅니다. 제한하는 자유도의 갯수에 따라 회전 조인트(revolute joint), 병진 조인트(translational joint) 등 부르는 형태도 다양합니다. 또한 기구학적 구속은 수식으로 나타낼 수 있는데요. 위 4절 기구를 예로 들면, 4절 기구의 꼭지점을 각각 경유하는 벡터 $\vec{O_2A}$, $\vec{AB}$, $\vec{BO_4}$, $\vec{O_4O_2}$의 합이 항상 0이면 각 꼭지점은 분리되지..

이번 포스팅에서는 파손 이론에 대한 내용 중 정적파손에 대해 먼저 알아보도록 하겠습니다. 파손(failure) 이론이란? 파손은 부품이 두개 혹은 그 이상으로 분리되거나 모양이 바뀌어 부품의 원래 기능을 제대로 할 수 없게 된 상태를 말합니다. 파손은 정하중 상태에서 발생하는 정적파손과 동하중 상태에서 발생하는 피로파손으로 나뉩니다. 그리고 파손 이론은 이러한 파손현상을 복잡한 형상의 부품으로 실험하지 않고 단축인장실험 데이터로 어떻게 입체에 써먹을까 하는 것을 말합니다. 정적 파손(static failure) 정적 파손에 대하여 일반적으로 잘 쓰이는 세가지 이론에 대해 알아보겠습니다. (1) 최대 전단응력 이론(maximum shear stress theory) 최대 전단응력 이론은 기계부품의 최대 전..

이번 포스팅에서는 재료의 파손을 설명하기 위한 이론 중 하나인 전단변형에너지 이론에 쓰이는 전단변형에너지 공식을 유도해보겠습니다. 전단변형에너지 이론? 전단변형에너지 이론은 von mises 이론이라고도 불리며, 재료의 파손을 설명하기 위해 제안된 이론 중 하나입니다. 재료의 파손에 대한 내용은 추후 포스팅에서 설명드리도록 하겠으며, 본 포스팅에서는 해당 이론에 쓰이는 전단변형에너지 공식을 유도해보겠습니다! 전단변형에너지 공식 유도 전단변형에너지를 알기 위해서는 총 변형에너지와 체적변형에너지를 알아야 합니다. 전단변형에너지는 총 변형에너지에서 체적변형에너지를 뺀 값이기 때문이죠! $$ 전단변형에너지 = 총 변형에너지 - 체적변형에너지$$ 총 변형에너지 3차원 응력 상태에서 총 변형에너지는 아래와 같습니다..

이번 포스팅에서는 본 미세스 응력에 대하여 알아봅시다. 본 미세스 응력(von mises stress)이란? 부르기에 따라 본 미세스 응력, 폰 미세스 응력이라고 부르기도 하는 이 응력은 흔히 등가응력(equivalent stress)으로 불리는 특수한 목적을 가진 응력입니다. 물체가 하중을 받게 되면 더 이상 외력을 견디지 못하고 파괴되는 시점이 오는데, 이러한 파괴를 예측하는 기준이 되는 응력을 항복응력(Yield stress)이라고 하며, 이 항복응력의 대표적인 기준으로써 본 미세스 응력이 쓰입니다. 예를 들어 특정 지점에서 각 3개의 normal stress, shear stress가 발생할 때 각 응력 성분들만으로는 물체가 외부하중에 의해 안전할지, 파괴될지를 판단할 수 없습니다. 이 때 각 응..