[동역학] 평면에서의 운동방정식 (with MATLAB)

이번 포스팅에서는 평면에서의 운동방정식에 대하여 알아보고,

 

구속이 포함된 운동방정식을 이용하여 단진자 운동 해석을 해보겠습니다.

 

 자코비안 행렬(jacobian matrix)

앞선 포스팅에서 우리는 기구의 구속식에 대해 알아보았습니다.

 

구속식은 기본적으로 body의 좌표로 이루어져있기 때문에,

 

초기값이 주어지면 해당 구속식을 풀어 기구의 상태를 확정할 수 있습니다.

 

운동방정식을 구성하기 위해서는 이 구속식을 미분하여 속도, 가속도를 구할 필요가 있는데요.

 

이 때 구속식을 각 좌표로 편미분하여 변화량을 구한 행렬을 자코비안 행렬(jacobian matrix)이라 합니다.

 

구속식이 존재하는 기구의 운동방정식을 구성하기 위해서는 이 자코비안 행렬이 필수적입니다.

 

예를 들어 Revolute joint의 자코비안을 구한다면

 

$$\Phi = \begin{bmatrix} x_i+\xi_i\cos\theta_i -\eta_i\sin\theta_i-x_j-\xi_j\cos\theta_j-\eta_j\sin\theta_j \\ y_i+\xi_i\sin\theta_i+\eta\cos\theta_i-y_j-\xi_j\sin\theta_j-\eta_j\cos\theta_j \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$

 

위 구속식을 각 좌표 $q = \left[x_i, y_i, \theta_i, x_j, y_j, \theta_j \right]^T$로 편미분하여 자코비안을 구합니다.

 

편의 상 $\Phi_q$라 표기하기로 하며, 자세히 쓰면 아래와 같습니다.

 

$$\Phi_q = \begin{bmatrix} 1 & 0 & -\xi_i\sin\theta_i-\eta_i\cos\theta_i & -1 & 0 & \xi_j\sin\theta_j+\eta_j\cos\theta_j \\ 0 & 1 & \xi_i\cos\theta_i-\eta_i\sin\theta_i & 0 & -1 & -\xi_j\cos\theta_j+\eta_j\sin\theta_j \end{bmatrix} $$

 

 위치, 속도, 가속도 해석

위에서 말한 것과 같이

 

초기값이 주어지면 구속식을 풀어 기구의 상태를 확정할 수 있습니다.

 

이 때 구속식을 미분하여 각각 속도, 가속도에 대한 풀이도 가능한데요.

 

일반적으로 구속식은 좌표 $q$와 시간 $t$의 함수입니다.

 

따라서 구속식을 시간에 대하여 미분했을 때 나오는 결과는 아래와 같습니다.

 

Position analysis

 

$$\Phi\left(q,t\right) = 0$$

 

위치에 대한 해석은 초기값이 주어졌을 때

 

newton-raphson법과 같은 비선형수치해석법으로 풀이 가능합니다.

 

Velocity analysis

 

$$\dot{\Phi}=\Phi_q \dot{q} + \Phi_t = 0$$

 

$\Phi_q$는 위에서 설명한 자코비안 행렬이고, $\dot{q}$는 좌표의 시간미분입니다.

 

기구의 운동을 특정 속도 등으로 움직이도록 하는 driving constraint가 없다면

 

$\Phi_t$는 0입니다.

 

마찬가지로 비선형수치해석법으로 풀이 가능합니다.

 

Acceleration analysis

 

$$\ddot{\Phi} = \left(\Phi_q\dot{q}+\Phi_t\right)_\dot{q} \ddot{q}+\left(\Phi_q\dot{q}+\Phi_t\right)_q\dot{q}+\left(\Phi_q\dot{q}+\Phi_t\right)_t=0$$

 

이 때 가속도항을 남기고 모든 항을 우항으로 넘겨 정리하면

 

아래와 같은 결과가 나오며, 이를 간단히 $\gamma$로 나타내기로 합시다.

 

$$\Phi_q\ddot{q}=-\left[\left(\Phi_q\dot{q}\right)_q\dot{q}+2\Phi_{qt}\dot{q}+\Phi_{tt}\right]=\gamma$$

 

이 역시 마찬가지로 초기값이 주어지면 비선형 수치해석법으로 풀이 가능합니다.

 

 평면(2D)에서의 운동방정식(Equations of motion)

평면에서의 운동방정식에 대해 알아봅시다.

 

평면(2D)에서 1개의 body는 3개의 자유도를 가지며,

 

각 좌표 축에 대한 평형방정식은 아래와 같습니다.

 

$$\Sigma F_x = ma_x$$

$$\Sigma F_y = ma_y$$

$$\Sigma M = I\alpha$$

 

따라서 구속이 없는 1-body system의 운동방정식은 아래와 같습니다.

 

$$\begin{bmatrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & I \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ \alpha \end{bmatrix} = \begin{bmatrix} F_x \\ F_y \\ M \end{bmatrix}$$

 

동일한 방법으로 구속이 없는 2-body system의 운동방정식은 아래와 같겠죠.

 

$$\begin{bmatrix} m_1 & 0 & 0 & 0 & 0 & 0 \\ 0 & m_1 & 0 & 0 & 0 & 0 \\ 0 & 0 & I_1 & 0 & 0 & 0 \\ 0 & 0 & 0 & m_2 & 0 & 0 \\ 0 & 0 & 0 & 0 & m_2 & 0 \\ 0 & 0 & 0 & 0 & 0 & I_2\end{bmatrix} \begin{bmatrix} a_{x_1} \\ a_{y_1} \\ \alpha_1 \\a_{x_2} \\a_{y_2} \\ \alpha_2 \end{bmatrix} = \begin{bmatrix} F_{x_1} \\ F_{y_1} \\ M_1 \\ F_{x_2} \\ F_{y_2} \\ M_2 \end{bmatrix}$$

 

그렇다면 구속이 존재하는 시스템의 운동방정식은 어떻게 구성할까요?

 

위에서 구해놓은 자코비안 행렬과 구속식의 미분 등으로 표현 가능합니다.

 

$$\begin{bmatrix} M & \Phi_q^T \\ \Phi_q & 0 \end{bmatrix} \begin{bmatrix} \ddot{q} \\ \lambda \end{bmatrix} = \begin{bmatrix} Q \\ \gamma \end{bmatrix} $$

 

여기서 $lambda$는 lagrange multiplier라고 하는데, 본문에서 설명은 생략하겠습니다.

 

$gamma$는 가속도 해석 시 구속식을 두번 미분했을 때 나왔던 바로 그 값입니다.

 

$Q$는 계에 작용하는 외력이 되겠죠.

 

우리는 위 식을 통해 시스템의 운동방정식을 나타낼 수 있습니다.

 

 예제 - single pendulum (MATLAB)

다뤄볼 예제는 single pendulum입니다.

 

위에서 구했던 revolute joint의 자코비안을 가지고 쉽게 구현할 수 있습니다.

 

수식에 대한 설명은 위에서 끝냈으니 바로 해보죠.

 

main script

clc; clear all; close all force;

%% pendulum 형상 정보
w_Gr = 0.1; d_Gr = 0.1;
w_pendulum = 2; d_pendulum = 0.1;

%%
pos_cm1 = [1, 0]';
rot_ang = 0;
rotA = Atrans(rot_ang);

q1_0 = [0, 0, 0]';
q2_0 = [(rotA*pos_cm1)', rot_ang]';

dq1_0 = [0, 0, 0]';
dq2_0 = [0, 0, 0]';

Y0 = [q1_0; q2_0; dq1_0; dq2_0];
dt = 0.01;
tspan = 0 : dt : 5;
t_end = tspan(2);

%% RK4 적분
Y = zeros(length(tspan),12);
t = zeros(length(tspan),1);
for i = 1 : length(tspan)
    t(i) = tspan(i);

    K1 = EOM_pendulum(t(i),Y0);
    K2 = EOM_pendulum(t(i)+dt*0.5,Y0+0.5*dt*K1);
    K3 = EOM_pendulum(t(i)+dt*0.5,Y0+0.5*dt*K2);
    K4 = EOM_pendulum(t(i)+dt,Y0+dt*K3);
    
    Y0 = Y0 + dt*(K1 + 2*K2 + 2*K3 + K4)/6;
    Y(i,:) = Y0;

end
%% ode45 적분
% opts = odeset('RelTol',5.e-003,'AbsTol',5.e-003);
% [t, Y] = ode45(@EOM_pendulum, tspan, Y0,opts);

%% 적분 결과(q, dq) EOM에 집어넣어서 dq, ddq 뽑아내기
len_data = length(Y);
len_coord = length(Y0);
dY = zeros(len_data,len_coord);

for j = 1 : len_data
    dY_tmp = EOM_pendulum(tspan(j),Y(j,:));
    dY(j,:) = dY_tmp;
end

%% 그래프 그리기
figure('units','normalized','pos',[0.05, 0.5, 0.35, 0.4])
subplot(311);
hold on; grid on;
plot(t,Y(:,4),'r');
xlabel('Time [sec]'); ylabel('Position - x [m]');
subplot(312);
hold on; grid on;
plot(t,Y(:,5),'r'); 
xlabel('Time [sec]'); ylabel('Position - y [m]');
subplot(313);
hold on; grid on;
plot(t,Y(:,6),'r');
xlabel('Time [sec]'); ylabel('Angle [deg]');

%% 애니메이션
pendulum_Animation;

 

운동방정식

function dY = EOM_pendulum(t,Y0)

g = 9.8; % m/s^2
dof = 3; % 2차원, 1 body 당 3자유도
num_body = 2; % ground, pendulum

s12_x_L = 0; s12_y_L = 0; s21_x_L = -1; s21_y_L = 0;

s12 = [s12_x_L, s12_y_L]'; s21 = [s21_x_L, s21_y_L]';

body(1).m = 1; body(1).j = 1;
body(2).m = 10; body(2).j = 10;

M = zeros(dof*num_body);

for i = 1 : num_body
    body(i).q = [Y0(3*i-2), Y0(3*i-1), Y0(3*i)]';
    body(i).dq = [Y0(3*i-2+dof*num_body), Y0(3*i-1+dof*num_body), Y0(3*i+dof*num_body)]';
    body(i).A = Atrans(body(i).q(3));
    body(i).F_gravity = [0, -body(i).m*g, 0]';
    body(i).F_ext = [0, 0, 0]';
    M(3*(i-1)+1:3*i,3*(i-1)+1:3*i) = diag([body(i).m,body(i).m,body(i).j]);
end


body(1).F_net = body(1).F_gravity + body(1).F_ext;
body(2).F_net = body(2).F_gravity + body(2).F_ext;
F_net = [body(1).F_net', body(2).F_net']';

[p_q_fix11, gamma_fix11] = Jac_fix(s12(1), s12(2), body(1).q(3), body(1).dq(3), s21(1), s21(2), body(2).q(3), body(2).dq(3), dof,num_body, 1);
[p_q_rev12, gamma_rev12] = Jac_rev(s12(1), s12(2), body(1).q(3), body(1).dq(3), s21(1), s21(2), body(2).q(3), body(2).dq(3), dof,num_body, 1);

p_q = [p_q_fix11', p_q_rev12']';
gma = [gamma_fix11; gamma_rev12];

ddq = [M, p_q';p_q, zeros(length(gma))]\[F_net', gma']';
dY = [body(1).dq', body(2).dq', ddq(1:6)']';

end

 

자코비안(fixed joint)

function [p_q, gamma] = Jac_fix(s_i_x,s_i_y,q_i_e,dq_i_e,s_j_x,s_j_y,q_j_e,dq_j_e,dof,num_body,connec)

s_ij = [s_i_x, s_i_y]';
s_ji = [s_j_x, s_j_y]';
A_i = Atrans(q_i_e);
A_j = Atrans(q_j_e);

p_q = zeros(3,dof*num_body);

p_q_tmp = [ eye(3,3), zeros(3,3) ];

p_q(:,3*(connec-1)+1:3*connec+3) = p_q_tmp;

gamma = [0, 0, 0]';

end

 

자코비안(revolute joint)

function [p_q, gamma] = Jac_rev(s_i_x,s_i_y,e_i,de_i,s_j_x,s_j_y,e_j,de_j,dof,num_body,connec)

s_ij = [s_i_x, s_i_y]';
s_ji = [s_j_x, s_j_y]';
A_i = Atrans(e_i);
A_j = Atrans(e_j);

p_q = zeros(2,dof*num_body);

p_q_tmp = [ 1.0, 0.0, -s_i_x*sin(e_i)-s_i_y*cos(e_i), -1.0, 0.0, s_j_x*sin(e_j)+s_j_y*cos(e_j);
            0.0, 1.0, s_i_x*cos(e_i)-s_i_y*sin(e_i), 0.0, -1.0, -s_j_x*cos(e_j)+s_j_y*sin(e_j)];

p_q(:,3*(connec-1)+1:3*connec+3) = p_q_tmp;

gamma = A_i*s_ij*de_i^2 - A_j*s_ji*de_j^2;

end

 

변환행렬

function A = Atrans(e)

A = [cos(e), -sin(e); sin(e), cos(e)];

end

 

애니메이션

x_Gr = [-w_Gr, -w_Gr, w_Gr, w_Gr]; 
y_Gr = [-d_Gr, d_Gr, d_Gr, -d_Gr];
x_pendulum = [-w_pendulum*pos_cm1(1)/w_pendulum, -w_pendulum*pos_cm1(1)/w_pendulum, w_pendulum*pos_cm1(1)/w_pendulum, w_pendulum*pos_cm1(1)/w_pendulum]; 
y_pendulum = [-d_pendulum/2, d_pendulum/2, d_pendulum/2, -d_pendulum/2];

figure('units','normalized','pos',[0.45, 0.5, 0.35, 0.4])
grid on;
hold on;
Gr = fill(x_Gr, y_Gr, 'k');
pendulum = fill(x_pendulum, y_pendulum, 'y');
hold off;
axis([-3 3 -3 3]);


% M = VideoWriter('Test.avi');
% open(M);
for j = 1 : len_data
   
    tmp_A1 = Atrans(Y(j,3));
    tmp_A2 = Atrans(Y(j,6));
    
    tmp_Gr = [Y(j,1), Y(j,2)]' + [tmp_A1*[x_Gr(1), y_Gr(1)]', tmp_A1*[x_Gr(2), y_Gr(2)]',tmp_A1*[x_Gr(3), y_Gr(3)]',tmp_A1*[x_Gr(4), y_Gr(4)]'];
    tmp_pendulum = [Y(j,4), Y(j,5)]' + [tmp_A2*[x_pendulum(1), y_pendulum(1)]', tmp_A2*[x_pendulum(2), y_pendulum(2)]',tmp_A2*[x_pendulum(3), y_pendulum(3)]',tmp_A2*[x_pendulum(4), y_pendulum(4)]'];
    
    
    updated_Gr = tmp_Gr;
    updated_pendulum = tmp_pendulum;
    
    set(Gr, 'Xdata', updated_Gr(1,:),'Ydata',updated_Gr(2,:));
    set(pendulum, 'Xdata', updated_pendulum(1,:),'Ydata',updated_pendulum(2,:));
    
    drawnow;
    
    for k = 1 : 5000000
        temp = k;
    end

%     frame = getframe();
%     writeVideo(M, frame);
end

% close(M);

 

위 코드를 실행한 결과는 아래와 같습니다.

 

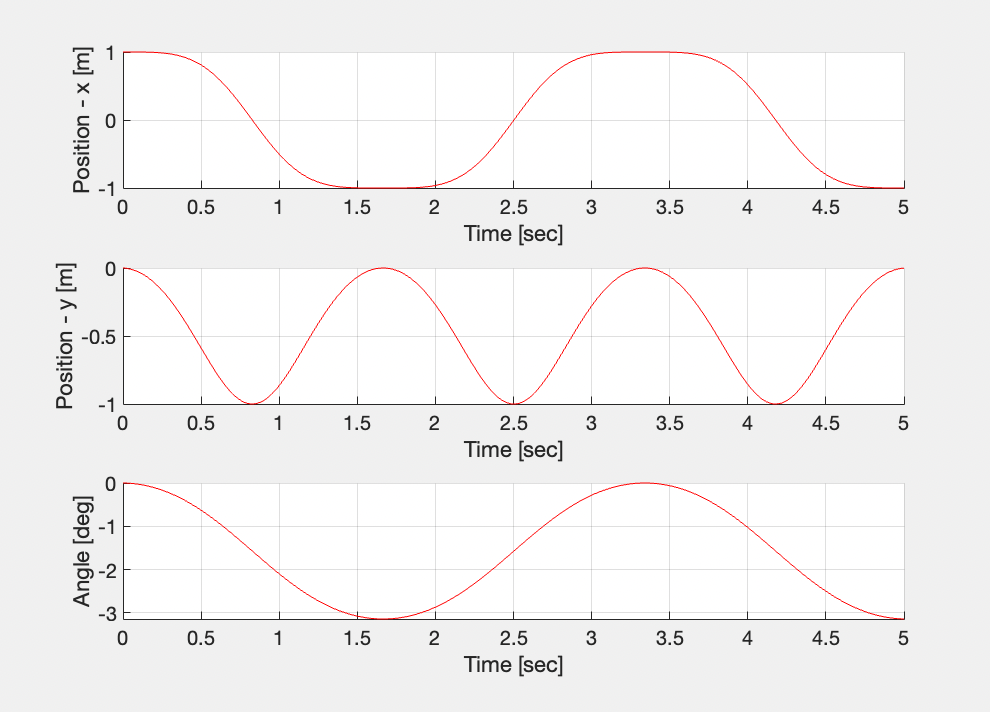
비교할 대상은 없지만...

 

잘 작동하는 것 같습니다.

 

여기까지 평면에서의 운동방정식과 구속이 포함된 운동방정식을 구성하는 방법,

 

그리고 간단한 예제의 실습까지 해보았습니다.

 

프로그래머가 아닌지라 code가 허접하긴 하지만 양해부탁드리며,

 

여기까지 포스팅을 마치겠습니다.

 

잘못된 내용에 대한 지적이나 가르침은 환영입니다!