공부해서 남주자

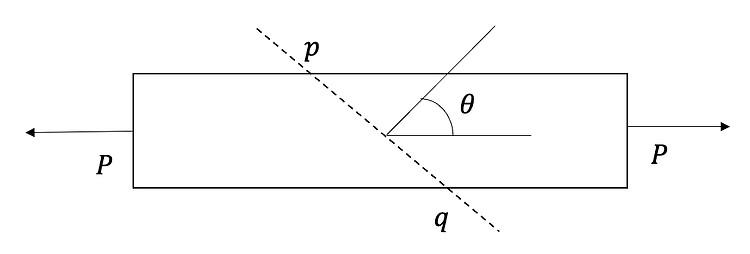
이번 포스팅에서는 순수전단(pure shear) 상태에 대해 알아보겠습니다. 순수전단(Pure shear) 우리는 비틀림을 받는 봉의 두 단면 사이를 잘라낸 응력요소를 고려하기 위해 순수전단(pure shear) 상태에 있는 구조물을 고려할 필요가 있습니다. 순수전단 상태에 있는 요소에 작용하는 유일한 응력은 아래 그림과 같이 네개 측면 위의 전단응력 $\tau$입니다. 여기서는 수직응력은 인장일 때 양(+), 전단응력은 수직면에 재료를 반시계방향으로 회젼시키려고 하는 힘을 양(+)으로 정의하겠습니다. 경사면에서의 응력 순수전단 상태에서는 응력 요소의 앞면과 뒷면에는 아무런 응력도 작용하지 않습니다. 따라서 모든 응력을 나타내면 아래그림과 같습니다. 경사면에서의 응력을 알고 싶을 때, 우리는 위 삼각형 ..

이번 포스팅에서는 비틀림(Torsion)에 대하여 알아보겠습니다. 비틀림(Torsion) 비틀림이란 봉의 길이방향 축에 대해 회전을 일으키려하는 모멘트에 의해 가해지는 현상을 말합니다. 만약 재료가 선형 탄성이면, 전단에 대한 훅의 법칙을 사용하여 비틀림 현상을 표현할 수 있습니다. 선형 탄성(linear elastic) 봉의 비틀림(torsion) 위에서 언급한대로, 만약 재료가 선형 탄성이면 전단에 대한 훅의 법칙을 사용할 수 있습니다. $$\tau = G\gamma$$ 여기서 $G$는 전단탄성계수이고 $\gamma$는 전단변형률입니다. 전단변형률을 좀 더 풀어서 식을 쓰면 아래와 같습니다. $$\tau _{max} = Gr\theta$$ $$\tau = G\rho\theta = \frac{\rho}..

이번 포스팅에서는 충격하중 시 봉의 최대 변형량과 응력에 대해 알아보겠습니다. 충격하중이 작용할 때의 변위 충격하중이 작용할 때 발생하는 봉의 최대 변위는 낙하질량에 의한 포텐셜 에너지 손실과 봉의 최대 변형에너지가 같다고 하는 에너지 보존 법칙으로부터 구할 수 있습니다. 포텐셜 에너지 손실은 $$E_{potential} = Mg(h+\delta _{max})=W(h+\delta _{max}) \tag{1}$$ 봉의 최대 변형에너지는 $$E_{deform} = \frac{EA\delta _{max}^{2}}{2L} \tag{2}$$ 여기서 식 (1)과 (2)가 같으므로, $$W(h+\delta _{max})=\frac{EA\delta _{max}^{2}}{2L}$$ 이는 $\delta _{max}$에 관..

이번 포스팅에서는 변형에너지에 대해 이야기해봅시다. 변형에너지란? 구조물에 하중이 작용하면 그 과정에서 하중 $P$는 천천히 길이 $\delta$만큼 이동하므로 그 양만큼의 일(work)을 하게 됩니다. 이 변형을 일으키기 위한 일을 하기 위한 능력을 변형에너지라 하며, 아래와 같이 계산할 수 있습니다. $$U=W=\int_{0}^{\delta} P_{1}d\delta _{1}$$ 식의 형태를 보면 아시겠지만 하중-변위선도에서 곡선 아랫부분이 변형에너지를 나타냅니다. 선형 탄성 변형(Linear elastic deformation)에서의 변형에너지 구조물의 재료가 훅의 법칙을 따르며 하중-변위 선도의 곡선이 직선이라고 가정하면, 구조물에 저장된 변형에너지 U는 아래와 같이 나타낼 수 있습니다. $$U=W..

이번 포스팅에서는 경사면에서의 응력이 어떤지에 대해 알아보겠습니다. 경사면에서의 응력요소 축하중을 받는 봉에 작용하는 응력의 상태를 표현할 때, 경사면에서는 어떤지에 대해서도 파악할 필요가 있습니다. 절단면에 작용하는 응력을 나타낼 때에는 경사면이 기울어진 각 $\theta$에 대해 나타낼 수 있습니다. 경사면에서의 응력 계산 그림 1에서의 단면 $pq$에 작용하는 응력을 구해보도록 하죠. 경사면 $pq$에 수직으로 작용하는 수직력 $N$과 접선방향으로 작용하는 전단력 $V$는 아래와 같이 계산됩니다. $$N=P\cos\theta \tag{1}$$ $$V=-P\sin\theta \tag{2}$$ 그리고 수직응력은 수직력 $N$을 단면적으로 나눈 것과 같고, 전단응력은 전단력 $V$를 단면적으로 나눈것과 ..

이번 포스팅에서는 부정정(statically indeterminate) 구조물이 무엇인지에 대해 알아보겠습니다. 부정정(statically indeterminate) 구조물 이란? 대개 스프링, 봉 등에 작용하는 하중에 대해 반력과 내부 축력 등은 자유물체도와 평형방정식만으로 구할 수 있습니다. 이러한 상태의 구조물을 정정(statically determinate) 구조물이라 합니다. 이러한 구조물의 힘은 재료의 성질을 알지 못하더라도 구할 수 있죠. 하지만 대부분의 현장에서 구조물은 이보다 복잡하며, 그들의 반력과 내부 축력 등은 정역학만으론 구할 수 없습니다. 이러한 구조물을 부정정(statically indeterminate) 구조물이라 하며, 아래의 예시와 같습니다. 위 구조물에 하중 $P$가 작..

이번엔 벡터의 내적(dot product)과 성질에 대해 알아보겠습니다. 벡터의 내적(dot product) 정의 벡터의 내적은 두 벡터의 관계 정의할 수 있습니다. 아래와 같은 두 벡터가 있다고 가정합시다. $$u = (u_{1},u_{2},...,u_{n}), v = (v_{1},v_{2},...,v_{n})$$ 그럼 내적(dot product)는 아래와 같이 정의됩니다. $$u·v=u_{1}v_{1}+u_{2}v_{2}+...+u_{n}v_{n}$$ 예를 들면, $$u=(1,2,3), v=(4,5,6)$$ 위 두 벡터에 대하여 내적을 구하면 아래와 같습니다. $$u·v=(1×4)+(2×5)+(3×6)=32$$ 내적(dot product)의 성질(properties) 내적에는 몇가지 유용한 성질이 있..

이번 포스팅에서는 선형대수방정식을 통해 curve fitting 하는 방법에 대해 알아보겠습니다. 임의의 점을 지나는 함수를 구할 때 - curve fitting 많은 경우에 우리는 특정 점을 지나는 함수를 구하고 싶은 경우가 있습니다. 그리고 이런 경우 대부분 함수를 다항함수(Polynomial)로 가정하여 구합니다. 예를 들어 $$(x_{1},y_{1}), (x_{2}, y_{2}), ... , (x_{n}, y_{n})$$ 위와 같은 n개의 점을 지나는 다항함수를 구할 때 미지수가 n개이므로 n-1차 다항함수로 fitting할 수 있습니다. 아래와 같이 다항함수의 경우 y절편까지가 미지수이기 때문이죠. $$y = a_{0} + a_{1}x + a_{2}x^{2} + ... + a_{n-2}x^{n-..

이번 포스팅에서는 선형대수방정식을 푸는 반복법 중 하나인 가우스-자이델(Gauss-seidel)법에 대해 알아보겠습니다. (출처: Chapra의 응용수치해석 3rd edition, Steven C. Chapra 저) 가우스-자이델(Gauss-Seidel)법 가우스-자이델 기법은 선형대수방정식을 푸는 반복법 중의 하나로, 제법 보편적으로 사용되는 방법입니다. 이 방법은 해를 구하기 위해 미지수 $x$을 가정해야 하며, 이를 연립방정식을 구성하는 각각 다른 방정식에 대입시켜 해를 수렴시켜가는 방법입니다. 초기값은 흔히 0으로 많이 시작합니다. 아래와 같이 주어지는 방정식이 있다고 해보죠. $$[A]\left\{x\right\}=\left\{b\right\}$$ 만약 이 방정식이 3x3라면, 각 해를 구하기 ..

이번 포스팅에서는 선형대수방정식을 풀기 위한 방법 중 하나인 LU decomposition/factorization (LU 분해법)에 대해 알아보겠습니다. (출처: Chapra의 응용수치해석 3rd edition, Steven C. Chapra 저) LU decomposition/factorization (LU 분해법)이란? 앞에서 살짝 말씀드렸듯이 LU 분해법 또한 선형대수방정식의 해를 구하기 위한 방법 중 하나입니다. 이전 포스팅에서 선형대수방정식을 풀기 위한 다른 방법인 Gauss elimination을 알아보았는데요. 우선 선형대수방정식의 일반적인 형태는 아래와 같습니다. $$[A]\left\{x\right\}=\left\{b\right\} \tag{1}$$ Gauss elimination은 분명..