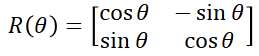공부해서 남주자

이번 포스팅에서는 회전 변환 행렬에 대해 알아봅시다. 회전 변환 행렬 (rotation matrix) 회전 변환 행렬이란, 좌표계에서 회전 변환을 할 때 사용하는 행렬을 말합니다. 2차원 직교좌표계에서 θ만큼 회전할 때, 변환 행렬은 아래와 같습니다. 유도 (derivation) 위 그림에서 점 P와 P'의 관계를 수식으로 나타낼 수 있다면 각 α에 대한 변환 행렬도 알아낼 수 있습니다. 먼저 점 P는 그리고 직선 OP와 점 x, y의 관계는 아래와 같습니다. 점 P'=(x', y')는 점 P를 +θ만큼 회전시킨 것이므로 아래와 같이 나타낼 수 있습니다. 이 식을 삼각함수의 덧셈 정리를 이용하여 풀어봅시다. 따라서 위 식을 정리하면 아래와 같습니다. 3D에서의 회전 변환 행렬 3차원에서도 2차원에서와 유..

이번 포스팅에서는 슈퍼개미 김정환님의 유튜브에서 다뤘던 적정주가 구하는 공식에 대해 알아보려고 합니다. 아래의 내용은 슈퍼개미 김정환님의 유튜브를 참고했음을 밝힙니다. (출처: youtu.be/RFwvU1bBu2o) 적정주가 만능공식 적정주가를 구하는 만능공식은 아래와 같습니다. 여기서 ROE는 자기자본이익률이라고 하며, 투입한 자본대비 얼마만큼의 이익을 냈는지를 나타내는 지표입니다. EPS는 주당 순이익으로써 기업이 벌어들인 순 이익을 총 주식수로 나눈 값이죠. 위 만능공식을 흔히 '주가가 고평가되었다'라고 판단하기 위해 사용되는 지표인 PER에 대한 식으로 나타내기 위해 양변을 EPS로 나눠봅시다. ROE = 적정 PER 이다. 즉, 기업 자본대비 이익률이 그 기업의 가치를 나타낼 수 있다는 내용입니..

이번 포스팅에선 요즘 이슈가 되고 있는 게임스탑 사건에 대해 알아봅시다. 게임스탑(GameStop Corp., NYSE, 종목코드: GME) 게임스탑은 미국의 비디오 게임 전문 소매 체인점입니다. 최근(21년 1월)에는 신형 Playstation 5와 Xbox series X가 출시되는 등 호재가 있어 주가에 긍정적으로 작용하고 있던 중이었습니다. 주가 폭등 원인 게임스탑은 오프라인 게임 유통이라는 특성 상 향후 전망이 좋진 않았습니다. 따라서 공매도 세력의 타겟이 되었고, 유명 헤지펀드들이 공개적으로 공매도하기 시작했죠. 그런데 이 공매도 물량을 분석해보니, 시가총액의 140%에 이르는 것을 투자자들이 확인한 것입니다. 이에 개인투자자들이 반발하여 "Buy and hold"를 외치며 게임스탑의 주식을 ..

미국 국채금리란? 먼저 국채란 무엇일까요? 국가가 돈을 빌리기 위해 발행한 채권을 말합니다. 그렇다면 미국 국채금리는 미국 정부가 채권을 발행해 돈을 빌릴 때의 금리를 말합니다. 미국 채권의 의의 누구나 돈을 빌려줄 때엔 갚을 수 있을만 한 사람에게만 빌려줍니다. 기업, 국가들은 돈을 빌릴 때에 채권을 발행해 채권의 금리만큼 이자를 주기로 약속하고 돈을 빌려오죠. 여기서 기업이 발행하는 채권은 회사채, 국가가 발행하는 채권은 국채입니다. 그렇다면 지구 상에서 돈을 빌려주면 절대로 안떼어먹을만 한 곳은 어디일까요? 바로 미국 정부입니다. 세계 경제가 위기에 빠지면 외국인들은 너나 나나 모두 투자금을 회수하여 미국으로 달려가죠. 그만큼 안전하다고 생각하기 때문입니다. 그렇기 때문에 미국의 국채금리는 다른 나..

맥놀이(Beat) 현상 맥놀이 현상이란 진동수가 비슷한 2개의 조화운동에 의해 진폭이 서서히 변화하는 진동을 말합니다. 두 조화운동을 합성할 때 진동수가 약간 다를때 일어나죠. 맥놀이 현상 예시 예를 들어봅시다. 아래 두 조화운동이 있다고 하죠 각각의 조화운동을 합성하면 아래와 같습니다. 위 식에서 보시는 바와 같이 합성된 운동은 각각 ω_1+ω_2의 진동수와 ω_1-ω_2의 진동수를 가집니다. 두 주파수는 유사하기 때문에, ω_1+ω_2는 원래 주파수의 거의 2배가 된 고주파로 작용하고, ω_1-ω_2는 거의 0에 가까운 저주파로 작용하게 됩니다. 따라서 두 주파수가 각각 저주파, 저주파로 나뉘어 운동의 진폭을 바꾸는 것이죠. 여기까지 맥놀이 현상에 대해 알아보았습니다.

월가의 전설로 불리는 피터린치에 대해 알아봅시다. 월스트리트의 전설적인 투자자, 피터 린치(Peter Lynch) 피터 린치는 월가의 전설로 불리우고 있습니다. 그 이유는 무엇일까요? 본인이 현역 펀드매니저로 활동했던 1977~1990년까지 약 13년의 기간동안 피델리티 인베스트먼트의 마젤란 펀드를 맡으며 연 평균 29.2%, 총 2700%에 달하는 어마어마한 수익률을 기록했기 때문인데요. 이 경이로운 수익률은 같은 기간 S&P500 지수 상승률의 두 배에 달하며, 월가에서 10년이 넘는 장기간동안 시장수익률을 능가한 경우는 피터 린치와 워렌 버핏을 제외하면 거의 없다고 합니다. 그래서 보통 월가의 3대장을 꼽으라면 이견이 거의 없이 조지 소로스, 워렌 버핏, 피터 린치를 꼽는다고 합니다. 투자관 피터 ..

이번 포스팅에서는 카스틸리아노의 정리에 대해 알아봅시다. 카스틸리아노의 정리(Castigliano's theorem) 카스틸리아노의 정리는 선형탄성계에서 변형에너지로부터 변위나 하중을 구하는 방법입니다. 제 1정리와 제 2정리 두가지가 있는데요, 카스틸리아노의 제 1정리 "어떤 탄성 구조물의 변형에너지를 변위의 함수로 나타낼 수 있다면, 변형에너지를 변위에 대해 편미분한 값은 하중과 같다." 고 하는 것입니다. 즉, 여기서 P=하중, U=변형에너지, δ=변위 입니다. 카스틸리아노의 제 2정리 어떤 탄성 구조물의 변형에너지를 하중의 함수로 나타낼 수 있다면, 변형에너지를 하중에 대해 편미분한 값은 변위와 같다."고 하는 것입니다. 즉, 이 방법을 활용하면, 변형에너지를 통해 쉽게 처짐량과 처짐각을 계산할 ..

이번 포스팅에서는 보의 처짐 공식 유도하는 법에 대해 알아봅시다. 보의 처짐 곡선 방정식 우선 처짐 공식을 유도하기위해 처짐 곡선 방정식부터 유도해봅시다. 처짐 곡선은 좌표 x에 대한 처짐량의 함수로 나타낼 수 있으며, 보의 각 지점에서 발생하는 처짐은 그 점에서의 곡률반경과 모멘트의 함수로써 아래와 같이 표현됩니다. 이 곡률에 관한 방정식과 보의 처짐 사이의 관계는 s1, s2점을 살펴보면 알 수 있는데요. s1점에서 그은 접선과 x축이 이루는 각을 θ, s2점에서 그은 접선과 x축이 이루는 각을 θ-dθ라 하면 그럼 각 s1-O-s2가 이루는 각은 dθ가 되죠. 즉, ds=ρdθ의 관계가 성립합니다. 따라서 그런데 여기서 실제 보의 처짐은 small deformation이기 때문에 라 할 수 있으므로..

이번 포스팅에서는 지난번 단면 1차모멘트에 이어 관성모멘트 및 극관성모멘트가 무엇인지에 대해 알아봅시다. 단면 1차 모멘트에 대해 궁금하신 분들은 아래 글을 참고하세요! [재료역학] 단면 1차 모멘트(First moment of area)와 도심(Centroid) 이번 포스팅에선 단면 1차모멘트와 도심에 대해 알아봅시다. 단면 1차모멘트와 도심 아래와 같은 그림에서 단면 1차모멘트에 대해 알아봅시다. 단면 1차모멘트는 축으로부터 도심점까지의 거 study2give.tistory.com 관성모멘트(Moment of inertia) 관성모멘트는 부재의 단면 모양에 의해 결정되는데, 단면의 성질에 따라 휨이나 처짐에 대한 저항을 말해줍니다. 단면 2차 모멘트라고도 합니다. 그렇기 때문에 각 축 방향에 따라 관..

이번 포스팅에선 단면 1차모멘트와 도심에 대해 알아봅시다. 단면 1차모멘트와 도심 아래와 같은 그림에서 단면 1차모멘트에 대해 알아봅시다. 단면 1차모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것인데요. 영어로는 First moment of area라고 합니다. 주로 도심을 구하고자 할 때 자주 계산합니다. 도심은 Centroid이죠. 단면 1차 모멘트는 각 축에 대해 존재하며, 구하는 방법은 아래와 같습니다. 여기서 x ̅, y ̅는 각 축방향의 무게중심입니다. 이 식에 의하면 축이 도심을 지날 때 단면 1차모멘트는 0이 됩니다. 그리고 이 식을 정리하면 단면 1차모멘트를 통해 아래처럼 무게중심을 계산할 수 있습니다. 여기서 A는 전체 면적입니다. 다양한 도형 형태에서의 도심 아래에 여러 도형에 ..