[재료역학] 파손(failure) 이론 - 정적 파손(static failure)

이번 포스팅에서는 파손 이론에 대한 내용 중

 

정적파손에 대해 먼저 알아보도록 하겠습니다.

 

 파손(failure) 이론이란?

파손은 부품이 두개 혹은 그 이상으로 분리되거나 모양이 바뀌어

 

부품의 원래 기능을 제대로 할 수 없게 된 상태를 말합니다.

 

파손은 정하중 상태에서 발생하는 정적파손과 동하중 상태에서 발생하는

 

피로파손으로 나뉩니다.

 

그리고 파손 이론은 이러한 파손현상을 복잡한 형상의 부품으로 실험하지 않고

 

단축인장실험 데이터로 어떻게 입체에 써먹을까 하는 것을 말합니다.

 

 

 정적 파손(static failure)

정적 파손에 대하여 일반적으로 잘 쓰이는 세가지 이론에 대해 알아보겠습니다.

 

 

(1) 최대 전단응력 이론(maximum shear stress theory)

 

최대 전단응력 이론은 기계부품의 최대 전단응력이

 

단순 인장시편의 최대 전단응력과 같을 때 항복이 일어난다는 이론입니다.

 

Tresca 이론이라고도 합니다.

 

단순인장 상태에서 항복이 일어날 경우 최대 전단응력은 아래와 같습니다.

 

$$\tau_{max}=\frac{\sigma_Y}{2}$$

 

여기서 $\sigma_Y$는 항복응력입니다.

 

그리고 일반적인 응력 상태에서 세 개의 주응력이 $\sigma_1 > \sigma_2 > \sigma_3$이라면

 

최대 전단응력 $\tau_{max}=\frac{\left\vert \sigma_1 -\sigma_3 \right\vert}{2}$ 이므로

 

최대 전단응력 이론은 아래와 같이 나타낼 수 있습니다.

 

$$\left\vert \sigma_1 -\sigma_3 \right\vert = \sigma_Y$$

 

만약 $\sigma_3 = 0$인 평면응력 상태라면, 최대 전단응력 이론은

 

$$\left\vert \sigma_1 -\sigma_2 \right\vert = \sigma_Y$$

 

이 되고, 이 식을 그래프로 나타내면 아래 영역과 같습니다.

최대 전단응력 이론의 안전영역과 항복경계

위 그래프의 안전영역은 탄성변형이 일어나는 재료가 안정한 영역이며,

 

바깥은 소성변형이 일어나는 불안정한 영역입니다.

 

경계선은 항복이 시작되는 시점을 의미합니다.

 

이 때, 최대 전단응력을 $\sigma_x$, $\sigma_y$, $\tau_{xy}$로 나타낸다면

 

아래와 같습니다.

 

$$\tau_{max}=\sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau_{xy}^2}$$

 

위 식은 모어 원(Mohr's circle)에서 쉽게 유도할 수 있습니다.

 

 

(2) 전단변형에너지 이론(distortion energy theory)

 

전단변형에너지 이론은 기계부품의 전단변형에너지가

 

단순 인장 시편의 전단변형에너지와 같을 때 항복이 일어난다는 이론입니다.

 

이 이론은 von Mises이론으로 불리며, 연성재료의 파손에 가장 많이 쓰이는 이론입니다.

 

전단변형에너지 이론의 안전영역과 항복경계

위 그래프에서 탄성변형이 일어나는 안전영역은 점선으로 나타낸 영역의 안쪽이며,

 

점선 밖은 소성변형이 일어나는 불안정한 영역입니다.

 

일반적으로 3차원 응력상태에서 전단변형에너지는 아래와 같이 나타낼 수 있습니다.

 

$$U_d = \frac{1+\nu}{3E}[\frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}{2}]$$

 

위 식을 구하는 과정은 아래 포스팅에 나타내었으니 참고하세요.

[재료역학] 전단변형에너지 공식 유도

 

그리고 단순인장 상태에서 전단변형에너지는 아래와 같습니다.

 

$$U_d = \frac{1+\nu}{3E}\sigma_Y^2$$

 

항복이 일어나는 조건은 위 두 식의 값이 같을 때 이므로,

 

$$\sigma_Y = [\frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}{2}]^{\frac{1}{2}}$$

 

이 때, $\sigma_Y=\sigma_{VM}$를 유효응력(effective stress) 혹은 von Mises 응력이라 합니다.

 

만약 평면응력 상태라면 $\sigma_3=0$이므로,

 

$$\sigma_{VM} = [\sigma_1^2-\sigma_1\sigma_2+\sigma_2^2]^{\frac{1}{2}}$$

 

와 같이 항복이 일어날 조건을 나타낼 수 있습니다.

 

 

(3) 최대 주응력 이론(maximum principal stress theory)

 

마지막으로 최대 주응력 이론은 Rankine 이론으로도 불리며,

 

어떤 부품의 최대 주응력이 단순인장 혹은 압축 시편의 최대 주응력과 같을 때

 

재료가 파단된다는 이론입니다.

 

그런데, 단순 인장 혹은 압축 시편에서의 최대 주응력은 그 극한강도인 인장강도와 같으므로,

 

$$\sigma_{max} = \sigma_u$$

 

로 나타낼 수 있습니다. 이 때, $\sigma_{max}$는 최대 주응력, $\sigma_u$는 인장강도 입니다.

 

주응력 $\sigma_1, \sigma_2$는 아래와 같이 나타낼 수 있으며

 

$$\sigma_{1,2} = \frac{\sigma_x+\sigma_y}{2}\pm \sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau_{xy}^2}$$

 

이 중 절대값이 큰 것이 최대 주응력이 됩니다.

 

최대 주응력 이론에 의한 안전영역은 아래와 같이 나타낼 수 있습니다.

최대 주응력 이론의 안전영역과 파단 경계

 

 

 

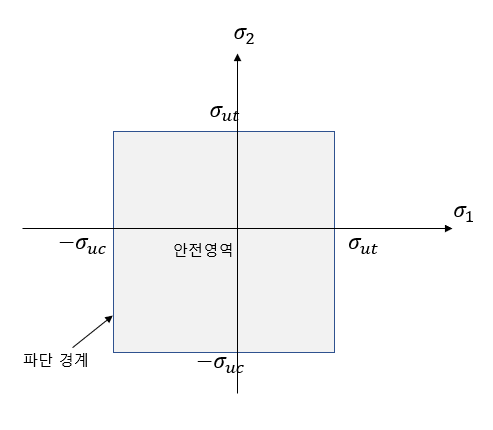
여기까지 대표적으로 쓰이는 3가지 파손이론에 대해 알아보았습니다.