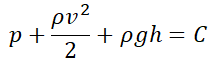공부해서 남주자

이번 포스팅에서는 등가스프링 상수 구하는 법에 대해 알아봅시다. 등가스프링 상수 구하는 이유 진동에서 계의 고유진동수는 질량 $m$과 강성$k$에 의해 결정되는 것을 아래의 포스팅을 통해 이미 알아본 바 있습니다. [기계진동] 공진(Resonance)과 고유진동수(Natural frequency) 이번 포스팅에서는 공진(Resonance)과 고유진동수(Natural frequency)에 대해 알아봅시다. 공진(Resonance)이란? 공진이란, 특정 주파수에서 사물이 큰 진폭으로 진동하는 현상입니다. 그 특정 주파수를 study2give.tistory.com 강성을 알아야 계의 고유진동수를 계산할 수 있고, 계에는 강성 요소가 복잡하게 얽혀있을 수 있기 때문에 하나의 값인 등가스프링 상수($k$)을 구하..

이번 포스팅에서는 수치적분법 중 하나인 사다리꼴 공식에 대해 알아봅시다. 사다리꼴 공식 정의 사다리꼴 공식은 적분이 나타내는 넓이를 사다리꼴의 형태로 나누어 그 넓이의 합으로 적분값을 근사하는 방법입니다. 위 그림과 같이 임의의 함수 $f$에 대해 적분값을 붉은색 사다리꼴 넓이의 합으로 나타내죠. 그렇기 때문에 경우에 따라 오차가 매우 크게 나타날 수 있습니다. 정의는 아래와 같습니다. 적분 가능한 함수 $f$에 대하여 이에 대한 적분 $F$는 $F = \sum_{i=0}^{N-1} \frac{(t_{i+1}-t_i)(f(t_{i+1})+f(t_i))}{2} \tag{1}$ 이 때, N=1인 경우 식은 아래와 같습니다. $F = \frac{(t_1-t_0)(f(t_1)+f(t_0))}{2} \tag{2}..

이번 포스팅에서는 레이놀즈 수에 대해 알아보도록 합시다. 레이놀즈 수(Reynold's number) 레이놀즈 수는 층류와 난류를 구분하는 척도가 되는 값으로, 일반적으로 $Re$로 표기하며 무차원의 수입니다. 여기서 층류(laminar flow)란, 유체 입자들이 질서정연하게 층과 층이 미끄러지면서 흐르는 유동상태를 말하며, 난류(turbulent flow)란, 유체 입자들이 불규칙하게 섞여서 흐르는 유동상태를 말합니다. 아무래도 난류 유동은 불규칙하기 때문에 유체역학적으로 층류에 비해 해석이 어렵습니다. 공식과 물리적인 의미 레아놀즈 수는 아래와 같은 공식으로 계산합니다. $Re=\frac{Vd}{ν}=\frac{\rho Vd}{\mu}$ 여기서, $\rho$ : 밀도 $(Ns^2/m^4)$ $d$ ..

이번 포스팅에서는 수치 적분 기법 중 하나인 Newmark method(뉴마크 기법)에 대해 알아보도록 하겠습니다. Newmark method(뉴마크 기법) 개요 Newmark method는 대표적인 implicit method 중 하나인데요. Nathan Mortimore Newmark(1910 - 1981)라는 사람에 의해 1959년 발표된 논문에 소개된 적분법입니다. ("A method of computation for structural dynamics", Journal of the Engineering Mechanics Division, 85 (EM3): 67–94) implicit method란 현재와 미래 시간의 시스템의 상태로부터 미래 시간의 상태를 계산하는 방법입니다. 반대말은 expli..

이번 포스팅에서는 테일러 급수에 대해 알아봅시다. Taylor's series(테일러 급수)의 정의 테일러 급수란, 원래의 함수를 도함수들의 한 점에서의 값으로 계산된 항의 무한합으로 나타내는 방법입니다. 그러한 성질을 가지고 있기 때문에 수치적분에서 많이 쓰이기도 합니다. 정의는 이러합니다. 함수 $f: R → R$이고, 임의의 실수 $a ∈ R$ 일 때, 테일러 급수는 아래와 같이 나타낼 수 있습니다. $f(x)=f(a)+f'(a)(x-a)+\frac{1}{2!}f''(a)(x-a)^2+\frac{1}{3!}f'''(a)(x-a)^3+...$ Taylor's series 유도 테일러 급수가 어떻게 나오는지에 대한 과정을 유도해보겠습니다. 미적분학의 기본정리로부터 $\int_a^xf'(t)dt=f(x)..

이번 포스팅에서는 좌굴(buckling)에 대해 이야기 해보겠습니다. 좌굴(buckling) 좌굴이란, 축 방향 압축력을 받는 부재가 그 수직방향으로 구부러지는 현상을 말합니다. 축 방향 힘을 받는데 횡방향으로 변형이 되니 바람직하지 않습니다. 또한 하중이 제거되어도 변형이 원복되지 않는 비탄성 거동을 보이기 때문에 구조물에 있어서는 안될 현상 중 하나입니다. 세장비와 오일러 공식 좌굴은 부재의 세장비(slenderness ratio)가 클수록 쉽게 발생하죠. 세장비는 기둥이 얼마나 가느다란가를 나타내는 값을 말합니다. 여기서 I는 단면2차 모멘트이고, A는 기둥의 단면적입니다. 또한 좌굴이 일어나지 않게 하기 위한 하중을 구하는 공식이 있습니다. 오일러 공식(Euler's formula)이라고 불리는 ..

이번 포스팅에서는 공진(Resonance)과 고유진동수(Natural frequency)에 대해 알아봅시다. 공진(Resonance)이란? 공진이란, 특정 주파수에서 사물이 큰 진폭으로 진동하는 현상입니다. 그 특정 주파수를 우리는 고유진동수(Natural frequency)라고 합니다. 각 사물은 그 물체만의 고유진동수를 가지고 있습니다. 또한 현실에서 사물의 고유진동수는 무한히 많습니다. 고유진동수의 개수는 자유도의 수만큼 존재하기 때문인데요. 이론으로 진동을 다룰 땐 사물을 이산화하여 다루기 때문에 그 갯수가 제한적이지만, 현실세계에서 사물은 모두 연속체이기 때문이죠! 정리하면, 고유진동수는 사물의 자유도의 갯수만큼 존재하며, 현실세계에선 무한히 많이 존재합니다. 고유진동수(natural frequ..

이번 포스팅에서는 피로(fatigue)에 대해 알아봅시다. 피로(fatigue) 피로는 재료가 재료의 항복강도보다 작은 응력을 반복적으로 받는 것을 말합니다. 비록 항복강도보다 작아 변형이 일어나지 않지만, 이렇게 작은 하중이어도 재료는 파괴될 수 있습니다. 재료가 피로로 인해 파괴되는 것을 피로파괴(fatigue failure)라고 합니다. 이 때, 하중이 무한대로 반복되어도 재료가 견딜 수 있는 응력의 범위를 피로한도(fatigue limit)라고 합니다. 위 그림은 S-N curve라고 부르는데, 이 곡선은 피로 하중에 의한 응력(S)와 반복 횟수(N)의 관계를 나타냅니다. 이 곡선은 재료마다 다르며, 각각의 곡선 데이터들을 얻기 위해서는 다수의 시편에서 측정되는 값을 취해야하기 때문에, 피로시험은..

이번 포스팅에서는 베르누이 방정식에 대해 다뤄보겠습니다. 베르누이 방정식 베르누이 방정식은 유체의 속도, 압력, 위치에너지 사이의 관계를 나타낸 식입니다. 유체에 대하여 하나의 유선(streamline) 상에서 모든 형태의 에너지 합은 항상 일정하다라는 점을 설명하고 있습니다. 여기서, p: 해당 점에서의 압력 ρ: 유체의 밀도 v: 해당 점에서의 속도 g: 중력 가속도 h: 기준면에 대한 높이 C: 상수(Constant) 입니다. 다만, 이 방정식은 몇가지 가정이 있어야만 성립합니다. 베르누이 방정식에서의 가정 베르누이 방정식이 만족되기 위해서는 크게 3가지 가정이 필요합니다. 1. 정상상태(steady state)여야 한다. 2. 비압축성(incompressible) 유체여야 한다. 3. 비점성(in..

이번 포스팅에서는 회전 변환 행렬에 대해 알아봅시다. 회전 변환 행렬 (rotation matrix) 회전 변환 행렬이란, 좌표계에서 회전 변환을 할 때 사용하는 행렬을 말합니다. 2차원 직교좌표계에서 θ만큼 회전할 때, 변환 행렬은 아래와 같습니다. 유도 (derivation) 위 그림에서 점 P와 P'의 관계를 수식으로 나타낼 수 있다면 각 α에 대한 변환 행렬도 알아낼 수 있습니다. 먼저 점 P는 그리고 직선 OP와 점 x, y의 관계는 아래와 같습니다. 점 P'=(x', y')는 점 P를 +θ만큼 회전시킨 것이므로 아래와 같이 나타낼 수 있습니다. 이 식을 삼각함수의 덧셈 정리를 이용하여 풀어봅시다. 따라서 위 식을 정리하면 아래와 같습니다. 3D에서의 회전 변환 행렬 3차원에서도 2차원에서와 유..