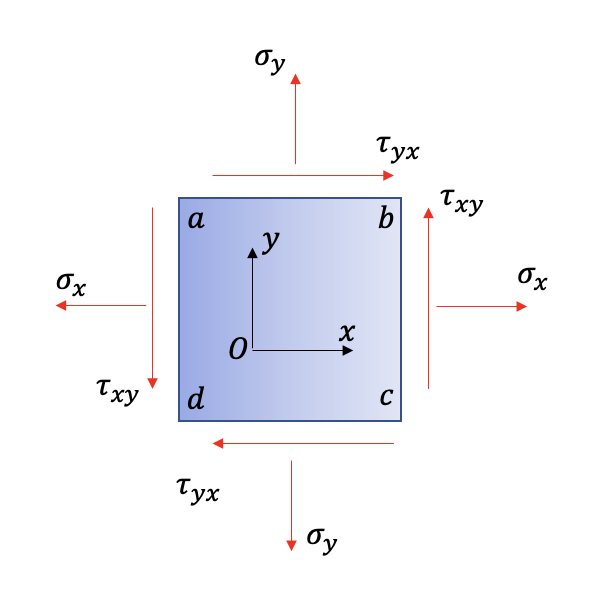
이번 포스팅에서는 응력 - 변형률 관계에 대해 알아보겠습니다. 3차원 응력 - 변형률 관계 육면체 요소가 존재한다고 가정했을 때, Hooke's law에 의하여 각 수직변형률, 전단변형률은 아래와 같이 쓸 수 있습니다. $$\epsilon_x = \frac{\sigma_x}{E}-\nu\frac{\sigma_y}{E}-\nu\frac{\sigma_z}{E}$$ $$\epsilon_y = -\nu\frac{\sigma_x}{E}+\frac{\sigma_y}{E}-\nu\frac{\sigma_z}{E}$$ $$\epsilon_z = -\nu\frac{\sigma_x}{E}-\nu\frac{\sigma_y}{E}+\frac{\sigma_z}{E}$$ $$\gamma_{yz} = \frac{\tau_{yz}}{..