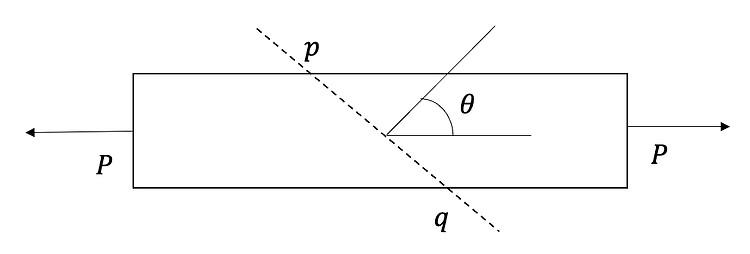
이번 포스팅에서는 경사면에서의 응력이 어떤지에 대해 알아보겠습니다. 경사면에서의 응력요소 축하중을 받는 봉에 작용하는 응력의 상태를 표현할 때, 경사면에서는 어떤지에 대해서도 파악할 필요가 있습니다. 절단면에 작용하는 응력을 나타낼 때에는 경사면이 기울어진 각 θθ에 대해 나타낼 수 있습니다. 경사면에서의 응력 계산 그림 1에서의 단면 pqpq에 작용하는 응력을 구해보도록 하죠. 경사면 pqpq에 수직으로 작용하는 수직력 NN과 접선방향으로 작용하는 전단력 VV는 아래와 같이 계산됩니다. N=Pcosθ V=−Psinθ 그리고 수직응력은 수직력 N을 단면적으로 나눈 것과 같고, 전단응력은 전단력 V를 단면적으로 나눈것과 ..