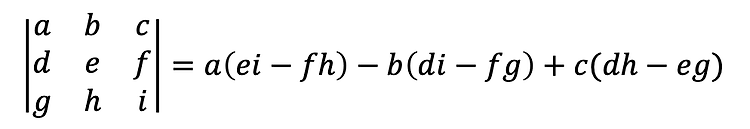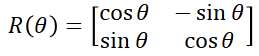공부해서 남주자

이번 포스팅에서는 행렬의 determinant에 대해 다뤄보겠습니다. 행렬식(Determinant) 행렬식이란, 어느 정사각행렬 $A$에 스칼라를 대응시키는 함수를 말하며, 본 행렬을 이용해 선형변환을 했을 때 그 크기의 배수를 말합니다. 구하는 방법은 여러가지가 있습니다만, 중고등학교때 $2$ x $2$ 행렬에 대하여 각 원소가 $a, b, c, d$일 때, $Det(A) = ad-bc$ 위와 같이 구하는 방법을 배운 바 있습니다. 행렬의 크기가 작으면 간단히 끝날 일이지만, $3$ x $3$ 이상으로 커지게 되면 일이 복잡해지는데요. 이런 경우엔 어떻게 구할 수 있을까요? 행렬식(Determinant) 구하는 방법 행렬식의 계산을 일반화해서 나타내면 아래와 같이 나타낼 수 있습니다. $Det(A) =..

이번 포스팅에서는 역행렬에 대해 다뤄보겠습니다. 역행렬(Inverse matrix)이란? $n$ x $n$행렬 $A$에 대하여, 곱하여 단위행렬이 나오게하는 행렬을 행렬 $A$의 역행렬이라 하며, 식으로 나타내면 아래와 같습니다. $A$ x $B$ = $B$ x $A$ = $I$ 여기서 $B$가 행렬 $A$의 역행렬입니다. 역행렬(Inverse matrix)을 구하는 방법 1. 가우스 - 조단 소거법(Gauss-jordan elimination method) 가우스 - 조단 소거법은 1) 역행렬을 구하고자 하는 행렬 $A$을 왼쪽 2) 단위행렬 $I$를 오른쪽에 두고 3) 각 행의 실수곱을 통해 왼쪽 행렬을 단위행렬로 만들면 4) 오른쪽에 역행렬 $B$가 나타납니다. 예를 들어 아래 $2$ x $2$ 행..

이번 포스팅에서는 회전 변환 행렬에 대해 알아봅시다. 회전 변환 행렬 (rotation matrix) 회전 변환 행렬이란, 좌표계에서 회전 변환을 할 때 사용하는 행렬을 말합니다. 2차원 직교좌표계에서 θ만큼 회전할 때, 변환 행렬은 아래와 같습니다. 유도 (derivation) 위 그림에서 점 P와 P'의 관계를 수식으로 나타낼 수 있다면 각 α에 대한 변환 행렬도 알아낼 수 있습니다. 먼저 점 P는 그리고 직선 OP와 점 x, y의 관계는 아래와 같습니다. 점 P'=(x', y')는 점 P를 +θ만큼 회전시킨 것이므로 아래와 같이 나타낼 수 있습니다. 이 식을 삼각함수의 덧셈 정리를 이용하여 풀어봅시다. 따라서 위 식을 정리하면 아래와 같습니다. 3D에서의 회전 변환 행렬 3차원에서도 2차원에서와 유..