[수치해석] Runge-kutta method(룽게-쿠타법) (with MATLAB)

이번 포스팅에서는 룽게-쿠타법에 대해 알아보도록 합시다.

 

(부르기에 따라 런지-쿠타, 룽게-쿠타 등 여러 발음으로 불리기도 하나,

 

본 포스팅에서는 룽게-쿠타로 표기하겠습니다.)

 

 룽게-쿠타법 (Runge-Kutta method)

룽게-쿠타법은 많은 수치적분법 중 한가지 방법입니다.

 

독일의 수학자 카를 다비트 톨메 룽게와 마르틴 빌헬름 쿠타가 개발하였고

 

흔히 4차항까지 구하여 사용하는 방법을 많이 쓰며,

 

이 방법은 RK4라고도 불립니다. 수치적분법 중 가장 흔히 사용되는 방법입니다.

 

식으로는 아래와 같이 나타낼 수 있습니다.

 

$$y_{i+1}=y_i+\frac{1}{6}(k_1+2k_2+2k_3+k_4)h$$

 

여기서 k는 아래와 같습니다.

 

$k_1=f(t_i, y_i)$

 

$k_2=f(t_i+\frac{1}{2}h, y_i+\frac{1}{2}k_1h)$

 

$k_3=f(t_i+\frac{1}{2}h, y_i+\frac{1}{2}k_2h)$

 

$k_2=f(t_i+h, y_i+k_3h)$

 

 유도(Derivation)

Taylor series로부터 $i+1$시점의 함수값 $y$는 아래와 같이 나타낼 수 있습니다.

 

$$y_{i+1}=y_i+\frac{dy}{dt}(t_{i+1}-t_i)+\frac{1}{2!}\frac{d^2y}{dt^2}(t_{i+1}-t_i)^2$$

$$+\frac{1}{3!}\frac{d^3y}{dt^3}(t_{i+1}-t_i)^3+\frac{1}{4!}\frac{d^4y}{dt^4}(t_{i+1}-t_i)^4+O(t_{i+1}-t_i)^n$$

 

여기서 $O(t_{i+1}-t_i)^n$은 $n^{th}$ error term이며,

 

만약 이 error가 충분히 작아 무시가능하다면 함수값 $y$는 아래와 같이 쓸 수 있습니다.

 

$$y_{i+1} \simeq y_i+f(t_i, y_i)h+\frac{1}{2!}f'(t_i, y_i)h^2+\frac{1}{3!}f''(t_i, y_i)h^3+\frac{1}{4!}f'''(t_i, y_i)h^3$$

 

그리고 RK4의 기본 형태인 아래와 같이 표현할 때

 

$$y_{i+1} = y_i+(a_1k_1+a_2k_2+a_3k_3+a_4k_4)h$$

 

$k_n$는 위에서 언급한것과 같이 아래와 같습니다.

 

$k_1=f(t_i, y_i)$

 

$k_2=f(t_i+\frac{1}{2}h, y_i+\frac{1}{2}k_1h)$

 

$k_3=f(t_i+\frac{1}{2}h, y_i+\frac{1}{2}k_2h)$

 

$k_2=f(t_i+h, y_i+k_3h)$

 

이건 RK4의 정의이기 때문에 왜이렇게 나오느냐? 라고 물어도 할 말이 없습니다.

 

위 공식을 통해 RK4의 컨셉을 말씀드리자면,

 

$dt=0, dt=h/2, dt=h$ 세 지점의 기울기 평균을 통해

 

다음 step의 값을 계산해내는 concept라고 생각하시면 되겠습니다!

 

RK4의 concept. 출처 - Numerical Methods for Engineers, 6th edition, Chapra, Canale

 

이 때, RK4의 기본형태에서 Taylor series와의 계수비교를 통해

 

$a_1$ ~ $a_4$를 확정할 수 있는데요.

 

전개가 꽤 복잡하니 천천히 따라오세요!

 

$k_1=f(t_i, y_i)$

 

$k_2=f(t_i+\frac{1}{2}h, y_i+\frac{1}{2}k_1h)=f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}f(t_i, y_i)$

 

$k_3=f(t_i+\frac{1}{2}h, y_i+\frac{1}{2}k_2h)=f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}\left[f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}f(t_i, y_i)\right]$

 

$k_4=f(t_i+h, y_i+k_3h)=f(t_i, y_i)+h\frac{d}{dt}\left[f(t_i,y_i)+\frac{h}{2}\frac{d}{dt}\left[f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}f(t_i, y_i)\right]\right]$

 

 

$y_{i+1}=y_i+(a_1k_1+a_2k_2+a_3k_3+a_4k_4)h$

 

$y_{i+1}=y_i+\left[a_1f(t_i, y_i)+a_2\left\{f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}f(t_i, y_i)\right\}\right]h$

              $+\left[a_3\left\{f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}\left[f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}f(t_i, y_i)\right]\right\}\right]h$

              $+\left[a_4\left\{f(t_i, y_i)+h\frac{d}{dt}\left[f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}\left[f(t_i, y_i)+\frac{h}{2}\frac{d}{dt}f(t_i, y_i)\right]\right]\right\}\right]h$

 

          $=y_i+(a_1+a_2+a_3+a_4)f(t_i, y_i)h+\left(\frac{1}{2}a_2+\frac{1}{2}a_3+a_4\right)f'(t_i, y_i)h^2$

          $+\left(\frac{1}{4}a_3+\frac{1}{2}a_4\right)f''(t_i, y_i)h^3+\frac{1}{4}a_4f'''(t_i, y_i)h^4 \tag{1}$

 

여기서 앞서 Taylor series에서 유도된 식을 이용하여 계수비교 합니다.

 

즉, 

 

$y_{i+1}=y_i+f(t_i, y_i)h+\frac{1}{2!}f'(t_i, y_i)h^2+\frac{1}{3!}f''(t_i, y_i)h^3+\frac{1}{4!}f'''(t_i, y_i)h^4 \tag{2}$

 

식 (1)과 식 (2)에서 각 $h^n$의 계수는 같아야 합니다.

 

식이 4개, 미지수가 4개이므로 우리는 여기서 $a_1$~$a_4$를 확정할 수 있습니다.

 

결과적으로 아래와 같이 나오며,

 

$$a_1 = \frac{1}{6}, a_2=\frac{1}{3}, a_3=\frac{1}{3}, a_4=\frac{1}{6}$$

 

따라서 RK4의 일반화된 형태는 아래와 같습니다.

 

$$y_{i+1} = y_i+\frac{1}{6}(k_1+2k_2+2k_3+k_4)h$$

 

 

 예제 (MATLAB)

간단한 미분방정식을 통해 룽게-쿠타법을 연습해봅시다.

 

$$y'+2y-3e^{-4t}=0$$

 

위의 1차 미분방정식을 풀어보도록 하죠.

 

참고로 exact solution은 아래와 같습니다.

 

$$y(t) = 2.5e^{-2t}-1.5e^{-4t}$$

 

룽게-쿠타법으로 근사해를 구한 결과와 정해를 서로 비교해볼겁니다.

 

우선 룽게-쿠타법을 위해 도함수를 구해보죠.

 

도함수는 미분방정식에서 두개 항을 이항하면 간단히 구할 수 있습니다.

 

$$f(t,y) = y' = 3e^{-4t}-2y$$

 

매트랩을 이용해 적분해봅시다!

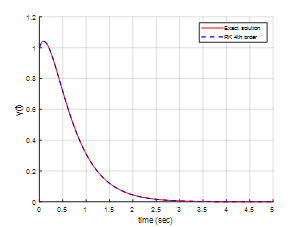
exact solution의 결과와 거의 오차없이 유사한 모습을 확인할 수 있습니다.

 

사용한 코드는 아래에 있습니다.

 

※ 미분방정식 함수

function dY = ODE_example(t,Y)

y = Y(1);

dY = 3*exp(-4*t)-2*y;

end

 

※ main script

clc; clear all; close all force;

%%

Y0 = 1;
  
%%

t_start = 0;
dt = 0.001;
t_end = 5;
n = t_end/dt+1;
Y = Y0;
Y_data = zeros(1,n);
t_data = zeros(1,n);

% exact solution
fn_y = @(t) 2.5*exp(-2*t) - 1.5*exp(-4*t);
exact_solution = zeros(1,n);

for i = 1 : n
    t = t_start + (i-1)*dt;
    
    K1 = ODE_example(t,Y);
    K2 = ODE_example(t+dt*0.5,Y+0.5*dt*K1);
    K3 = ODE_example(t+dt*0.5,Y+0.5*dt*K2);
    K4 = ODE_example(t+dt,Y+dt*K3);
    
    Y = Y + dt*(K1 + 2*K2 + 2*K3 + K4)/6;
    
    Y_data(:,i) = Y;
    t_data(:,i) = t;
    
    exact_solution(:,i) = fn_y(t);
end
%% solution

figure; hold on; grid on;
plot(t_data,exact_solution,'r-','LineWidth',2)
plot(t_data,Y_data,'b--','LineWidth',2)
legend('Exact solution','RK 4th order')
xlabel('time [sec]'); ylabel('y(t)');

 

이상으로 룽게-쿠타법에 대해 알아보았습니다.