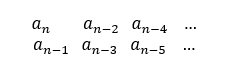공부해서 남주자

이번 포스팅에서는 제어시스템의 안정도에 대해 알아보겠습니다. 안정도 조사법 '시스템이 안정하다'라는 말은, 시스템이 한정된 응답을 가질 때를 말합니다. 즉, 한정된 입력이 가해졌을 때 그 응답의 크기가 한정되는 상황을 말합니다. 선형시스템의 경우 시스템의 특성방정식의 근을 조사하여 시스템이 안정한지 불안정한지를 판단할 수 있습니다. 특성방정식을 이용한 안정도 판별법 아래와 같은 전달함수 $G(s)$에 대하여 생각해봅시다. $$G(s) = \frac{N(s)}{D(s)} = \frac{K(s-z_1)(s-z_2)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)}$$ 위 전달함수의 특성방정식의 근 $p_i$ $(i=1,2,...,n)$이 시스템의 안정도를 결정합니다. 위 시스템에 단위스텝입력..

본 포스팅에서는 시스템의 정상상태응답에 대해 알아보겠습니다. 정상상태응답(steady-state response)이란? 정상상태응답이란 시스템이 안정되어 그 응답이 일정한 값을 유지하는 상태의 응답을 말합니다. 앞서 과도응답상태에 대해 다룬 포스팅에서 정착시간 $t_s$ 이후의 응답을 의미합니다. 정상상태응답 해석 정상상태응답을 해석하기 위해서는 우선 기준입력에 대한 오차를 고려해야 합니다. 오차를 구할 수 있다면 기준입력으로부터 정상상태응답 또한 계산할 수 있죠. 또한 정상상태에서 오차가 크면 시스템의 성능이 만족스럽다고 할 수 없기 때문에 정상상태오차를 분석하는 것이 필요합니다. 아래와 같은 폐루프 시스템에 대하여 정상상태오차를 계산해봅시다. 위 폐루프 시스템의 오차신호 $e(s)$는 아래와 같이 계..

이번 포스팅에서는 지난 포스팅에 이어 2차 시스템의 과도응답에 대해 알아보겠습니다. 2차 시스템의 전달함수 $G(s)$ 다음과 같은 전달함수 $G(s)$로 표현되는 2차 시스템에 대해 생각해봅시다. $$G(s) = \frac{\omega_n^2}{s^2+2\zeta\omega_n s+\omega^2}$$ 이 때 $\zeta$는 감쇠비(damping ratio), $\omega_n$는 고유주파수(natural frequency)입니다. 단위스텝입력에 대한 2차 시스템의 응답 여기에 단위스텝입력 $u(s) = 1/s$를 가했을 때 시스템의 출력 $y(s)$는 $$ y(s) = \frac{\omega_n^2}{s(s^2+2\zeta\omega_n s+\omega^2)}$$ 라플라스 변환표를 활용하여 위 출력 ..

이번 포스팅에서는 시스템의 과도응답에 대해 알아보겠습니다. 과도응답(transient response) 과도응답이란 출력이 정상상태(steady state)가 되기전까지 걸리는 시간에 나타나는 응답을 말합니다. 과도응답이 나타나는 중에는 일반적으로 출력신호가 파형을 그리며 변하게 되죠. 만약 시스템이 안정하다면 특정 입력신호에 대한 시간응답을 가지고 시스템의 성능을 평가할 수 있는데요. 일반적으로 - 임펄스함수(impulse function) - 스텝함수 (step function) - 램프함수 (ramp function) 등에 대한 응답을 분석함으로써 시스템의 성능을 평가합니다. 본 포스팅에서는 스텝함수의 입력에 대한 응답을 아래에서 좀 더 세밀히 다뤄보겠습니다. 임펄스(impulse) 입력에 의한 시..

이번 포스팅에서는 전달함수의 영점과 극점에 대해 알아보겠습니다. 전달함수(transfer function)란? 전달함수는 선형 시불변(linear time-invariant) 시스템을 주파수역에서 해석할 수 있도록 시스템의 입력과 출력 사이의 동특성을 식으로 나타내어 만든 것입니다. 아래와 같이 전달함수 $G(s)$는 입력 $u(t)$와 출력 $y(t)$의 라플라스 변환으로 나타낼 수 있습니다. $$G(s) = \frac{y(s)}{u(s)}=\frac{N(s)}{D(s)}$$ 여기서 전달함수는 시스템의 모든 초기조건이 0이라고 가정합니다. (입력에 의한 출력의 영향을 보기 위한 시스템이기 때문) 영점(zero)와 극점(pole) 전달함수 $G(s)$에서 분모의 다항식 $D(s)$를 특성다항식이라 하고,..