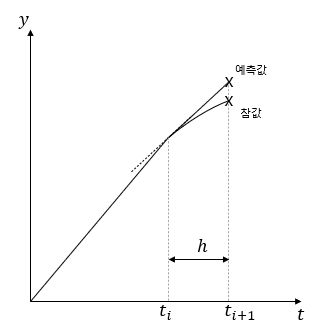
이번 포스팅에서는 미분방정식을 푸는 방법 중 하나인 오일러(Euler)법에 대하여 알아봅시다. (출처: Chapra의 응용수치해석 3rd edition, Steven C. Chapra 저) 오일러(Euler)법 오일러법은 초기값과 ii번째 1차 도함수의 기울기를 이용하여 i+1번째 함수값을 예측하기 위한 방법입니다. 식과 그림으로 나타내자면 아래와 같습니다. yi+1=yi+f(ti,yi)h 식과 그래프를 보면 알 수 있다시피 시간격 h에 대하여 선형외삽하는 방법입니다. 오일러(Euler)법의 오차 분석 오차 분석을 위해 오일러법을 유도하기 위한 Taylor급수 전개를 살펴봅시다. $$y_{i+1}=y_i+y'_i h+\frac{y''_i}{2!}h^2+...+\frac{y^n..