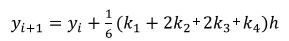이번 포스팅에서는 수치적분법 중 하나인 사다리꼴 공식에 대해 알아봅시다. 사다리꼴 공식 정의 사다리꼴 공식은 적분이 나타내는 넓이를 사다리꼴의 형태로 나누어 그 넓이의 합으로 적분값을 근사하는 방법입니다. 위 그림과 같이 임의의 함수 $f$에 대해 적분값을 붉은색 사다리꼴 넓이의 합으로 나타내죠. 그렇기 때문에 경우에 따라 오차가 매우 크게 나타날 수 있습니다. 정의는 아래와 같습니다. 적분 가능한 함수 $f$에 대하여 이에 대한 적분 $F$는 $F = \sum_{i=0}^{N-1} \frac{(t_{i+1}-t_i)(f(t_{i+1})+f(t_i))}{2} \tag{1}$ 이 때, N=1인 경우 식은 아래와 같습니다. $F = \frac{(t_1-t_0)(f(t_1)+f(t_0))}{2} \tag{2}..
