[머신러닝] 아핀 셋(affine set)과 컨벡스 셋(convex set)

이번 포스팅에서는 아핀 셋(affine set)과 컨벡스 셋(convex set)에 대하여 알아보겠습니다.

 

저도 잘 모르는 분야라 이제부터 교재를 통해 공부해보려고 합니다..

 

본 포스팅은 아래의 출처를 참고하였습니다.

(출처: 선형대수와 통계학으로 배우는 머신러닝 with 파이썬, 장철원 지음)

 

 직선과 선분

아핀 셋과 컨벡스 셋을 알아보기에 앞서 직선과 선분에 대해 먼저 알아보겠습니다.

 

직선(line)과 선분(line segment)는 비슷한 것 같지만 다릅니다.

 

직선은 시작과 끝 지점이 존재하지 않는 반면, 선분은 시작과 끝 지점이 존재합니다.

 

공간 $R^n$에서 두 점 $x_1, x_2$를 잇는 선을 아래와 같이 표현해보겠습니다.

 

$$y=wx_1+(1-w)x_2$$

 

위 식에서 만약 $w=0$이면 $y=x_2$가 되고, $w=1$이면 $y=x_1$이 됩니다.

 

만약 $0 \leq w \leq 1$이면 $y$는 $x_1, x_2$를 잇는 선분이 되고,

 

$w\in R$이면 직선이 됩니다.

 

 아핀 셋(affine set)

2차원 공간에서 집합 $C$ 내부의 두 점을 잇는 직선이 있다고 가정할 때

 

$wx_1+(1-w)x_2 \in C$이면 집합 $C$는 아핀 셋입니다.

 

아핀 셋은 시작과 끝 범위 제한이 없는 직선을 포함하므로,

 

아핀 셋 또한 범위 제한이 없습니다.

아핀 셋 영역

만약 2차원이 아니라 $n$차원이라면 $w_1x_1+w_2x_2+...+w_nx_n$으로 쓸 수 있고,

 

이를 포인트 $x_1, x_2, ... x_n$에 대한 아핀 조합(affine combination)이라고 합니다.

 

이 때, $w_1 + w_2 + ... + w_n = 1$을 만족합니다.

 

아핀 조합은 곧 집합 $C$에 속하는 점들의 선형 결합(linear combination)과 같습니다.

 

 아핀 함수와 선형 함수의 차이

$n$차원에서 $m$차원으로 차원을 변환하는 함수 $f: R^n → R^m$이 존재한다고 해봅시다.

 

위 함수 $f$의 의미는 $n$차원 공간 $R^n$에 속하는 벡터를

 

$m$차원 공간 $R^m$에 속하는 벡터로 변환한다는 의미입니다.

 

함수 $f$가 선형 변환이라면 $n \times m$ 행렬로 나타낼 수 있고, 이를 $W$라 하면

 

$$f(x) = Wx$$

 

데이터 포인트 $x$를 선형 변환하는 선형 함수는 위와 같은 식으로 나타낼 수 있습니다.

 

여기서 아핀 함수가 선형 함수와 다른 점 하나가 있는데요.

 

아핀 함수는 여기에 상수항 $b$가 추가된다는 것입니다.

 

$$f(x) = Wx+b$$

 

선형 부분 공간 vs 아핀 부분 공간

선형 변환을 통해 만들어진 선형 부분 공간은 원점을 지나지만,

 

아핀 변환을 통해 만들어진 아핀 부분 공간은 상수 $b$에 의해

 

$y$ 절편 $b$를 지나는 것을 확인할 수 있습니다.

 

 컨벡스 셋(convex set)

만약 집합 $C$ 내부의 두 점 사이의 선분이 집합 $C$에 속한다면

 

집합 $C$는 컨벡스(convex)합니다.

 

즉, 두 점 $x_1, x_2 \in C$에 대해 $0\leq w\leq 1$을 만족하는 $w$에 대하여

 

아래 조건을 만족하면 집합 $C$를 컨벡스 셋이라고 합니다.

 

$$wx_1+(1-w)x_2 \in C$$

 

눈치 채셨겠지만 컨벡스 셋은 두 점을 잇는 직선을 포함하는 아핀 셋과는 달리

 

두 점 사이의 선분을 포함합니다.

 

컨벡스 셋 개념

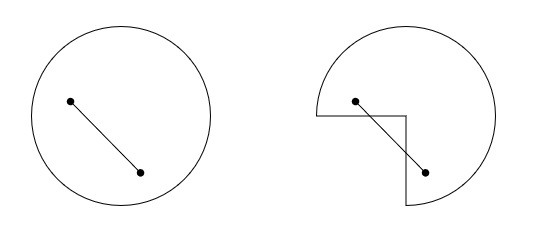
위 그림에서 왼쪽은 컨벡스 셋이지만 오른쪽은 컨벡스 셋이 아닙니다.

 

오른쪽 그림은 두 점 사이의 선분 내 점들이 모두 도형에 속하지 않기 때문입니다.

 

이 때, 아핀 셋은 두 지점 사이의 모든 선을 포함하므로

 

자연스럽게 두 점 사이의 모든 선분 또한 포함하기 때문에

 

아핀 셋이면 컨벡스 셋이라고 말할 수 있습니다.

 

그리고 데이터 포인트 $w_1x_1+w_2x_2+...+x_nx_n$이 존재할 때,

 

이를 $x_1,...x_n$의 컨벡스 조합(convex combination)이라고 합니다.

 

이 때, $w_1+...+w_n=1$이며, $w_1,...,w_n >0$을 만족해야 합니다.

 

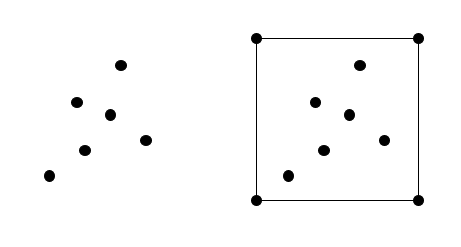
그리고 컨벡스 헐(convex hull)이라는 개념이 있는데요.

 

컨벡스 셋이 집합 내부의 두 점 사이 선분을 통해 컨벡스 여부를 알아보았다면

 

컨벡스 헐은 주어진 점들을 포함하는 컨벡스 셋을 의미합니다.

 

컨벡스 헐의 개념

 

여기까지 아핀 셋(affine set)과 컨벡스 셋(convex set)에 대하여 알아보았습니다.